技術士試験(情報工学部門)・情報技術者試験。ファーストマクロ。

�W−１８

二次元座標変換を、同次座標を用いて以下の式のように表すとき、下図のように点 (10, 10) を中心に反時計回りに90°回転させる座標変換を表す変換行列 Ｍ として正しいものはどれか。

---

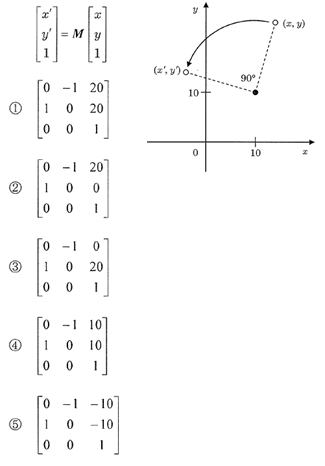
類題

H19 �W-15

---

正解

�A

---

解説

高校数学の幾何 (数学B) の問題である。
点 (x, y) を原点の周りに角度θだけ回転させた時、回転後の座標を (x', y') とすると、次のとおりとなる。
x' = x・cosθ - y・sinθ
y' = ｘ・sinθ + y・cosθ

点 (10, 10) を中心に90°回転させるので

x' = (x-10)・cos90°- (y-10)・sin90° + 10
　= 0 - (y-10) + 10 = -y + 20
y' = (x-10)・sin90° + (y-10)・cos90° + 10
　= x-10 + 0 +10 = x

�W−１７

目次

�W−１９

---