問2
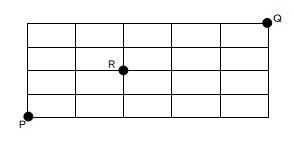
図の線上を、点Pから点Rを通って、点Qに至る最短経路は何通りあるか。
正解
エ
解説
高校数学の確率統計の問題である。PからRまでは、左右方向の経路と上下方向を経路の組合せであり、その経路は4C2 = 6通りある。実際には
−−┃┃
−┃−┃
−┃┃−
┃┃−−
┃−┃−
┃−−┃
の6通りである。
RからQまでも同様に、その経路は5C3通りある。
従って点Pから点Rを通って、点Qに至る最短経路は
4C2 × 5C3 = (4×3)/(2×1) × (5×4×3)/(3×2×1)
= 6×10 = 60通り。