平成23年度 秋期 応用情報技術者試験問題と解説
問8
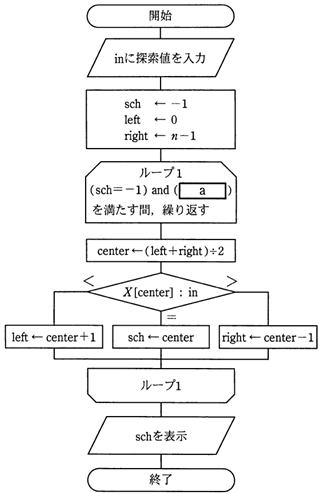
データが昇順にソートされた配列 X[i] (i = 0、 1、...、n−1) を2分探索する。流れ図の a に入るものとして、適切なものはどれか。ここで、流れ図の中の割り算は小数点以下を切り捨てるものとする。
ア left < right
イ left ≦ right
ウ left +1 < right
エ left +1 ≦ right
正解
イ
解説
2分検索法は検索値と、データを2分割した真ん中の値を比較し、検索値がデータの真ん中の値よりも小さければ、データの前半部分を、大きければデータの後半部分を検索して、検索範囲を2分の1ずつ狭めていく方法である。
例えば
n = 4
X[0] = 0、 X[1] = 1、 ・・・ X[3] = 3
探索値 in = 4 のとき
sch = -1 left = 0, rigth = 3
ループ1回目
center = (0+3)÷2 = 1
X[1] = 1 < 4 なので
left = 1+1 = 2
ループ2回目
center = (2+3)÷2 = 2
X[2] = 2 < 4 なので
left = 2+1 = 3
ループ3回目
※このとき left = 3, rigth = 3 であり、
まだ、X[3]が探索できておらず、ループする必要がある。条件として
ア left < right は、3<3が偽となりループ終了。(不適切)
ウ left+1 < right は、3+1<3 が偽となりループ終了。(不適切)
エ left+1 ≦ right も、3+1≦3 が偽となりループ終了。(不適切)
イ left ≦ right は 3≦3 が真となるため、ループが続く。
center = (3+3)÷2 = 3
X[3] = 3 < 4 なので
left = 3+1 = 4
探索X[3]が終了しためループは終了しなければならない。
条件 left ≦ right が 4 ≦ 3 で偽となるため、ループは終了する。
従って a には left ≦ right が入る。
| 問7 | 目次 | 問9 |