平成23年度 技術士第一次試験問題【専門科目】
Ⅳ-18
下図において、ノード a からノード h の間の最短距離はどれか。ただし、図中の数字は隣接する各ノード間の距離とし、任意の2点間の距離は各ノード間距離の和とする。
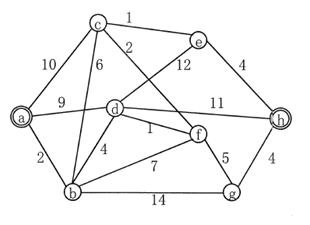
① 12 ② 13 ③ 14 ④ 15 ⑤ 16
正解
②
解説
a から c への経路は a → c と a → b → c があり、a → c だと距離は10だが、a → b → c だと距離は 8 である。従って a から c までの最短距離は8である。
同様にして、a から d までの最短距離は6である。
さらに同様に考えて
a から e までの最短距離は9。
a から f までの最短距離は7。
a から g までの最短距離は12。
a から h までの最短距離は
a → b → c → e → h で13である。
上記のように各点までの距離を順番に確定していくアルゴリズムをダイクストラ法という。
| Ⅳ-17 | 目次 | Ⅳ-19 |