令和6年度 春期 応用情報技術者試験問題と解説
問1
複数の袋からそれぞれ白と赤の玉を幾つかずつ取り出すとき、ベイズの定理を利用して事後確率を求める場合はどれか。
ア ある袋から取り出した二つの玉の色が同じと推定することができる確率を求める場合
イ 異なる袋から取り出した玉が同じ色であると推定することができる確率を求める場合
ウ 玉を一つ取り出すために、ある袋が選ばれると推定することができる確率を求める場合
エ 取り出した玉の色から、どの袋から取り出されたのかを推定するための確率を求める場合
正解
エ
解説
ベイズの定理は、事前に持っている事前確率と新しいデータから、事後確率を計算する手法である。
ベン図で書くと ①÷(①+②)の確率である。
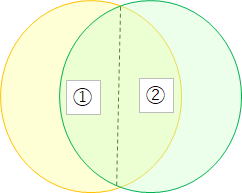
「黄色の袋には玉が300個、緑の袋には玉が700個入っている。
黄色の袋には当たりの赤い玉が5%、緑の袋には赤い玉が3%入っている。
どちらかの袋から赤い玉を取り出した時、黄色の袋から取り出した確率を求めよ。」
というような場合に用いる。
ちなみに、
「病気Xの人は人口の1%、病気Xでない人は人口の99%である。
病気Xで陽性反応が出る確率が90%、病気Xでないのに陽性反応が出る確率が5%である。
検査を受けて陽性と診断された場合、病気Aにかかっている確率を求めよ。」
というような場合でも用いられる。
答えはそれぞれ以下のとおり。
(0.05×0.3) ÷ (0.05×0.3 + 0.03×0.7) = 0.417
(0.9×0.01) ÷ (0.9×0.01 + 0.05×0.99) = 0.15
| 目次 | 問2 |