令和元年度 秋期 基本情報技術者試験問題と解説
問1
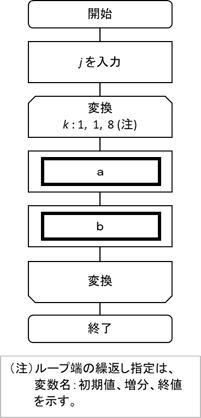
次の流れ図は、10進整数 j (0 < j <100) を8桁の2進数に変換する処理を表している。2進数は下位桁から順に、配列の要素
NISHIN(1) から NISHIN(8) に格納される。流れ図のa及び bに入れる処理はどれか。ここで、j div 2 は j を2で割った商の整数部分を、j
mod 2は i を2で割った余りを表す。
┌─────────┬─────────┐
│ a │ b │
┌─┼─────────┼─────────┤
│ア│j←j div 2 │NISHIN(k)←j mod 2│
├─┼─────────┼─────────┤
│イ│j←j mod 2 │NISHIN(k)←j div 2│
├─┼─────────┼─────────┤
│ウ│NISHIN(k)←j div 2│j←j mod 2 │
├─┼─────────┼─────────┤
│エ│NISHIN(k)←j mod 2│j←j div 2 │
└─┴─────────┴─────────┘
正解
エ
解説
J = 10 として考える。2進数では 00001010 であるから、
NISHIN(1) = 0
NISHIN(2) = 1
NISHIN(3) = 0
NISHIN(4) = 1
NISHIN(5) = 0
NISHIN(6) = 0
NISHIN(7) = 0
NISHIN(8) = 0
となればよい。
ア
j = 10
1回目
a: j ← 10 div 2 = 5
b: NISHIN(1) ← 5 mod 2 = 1
この時点で誤り。
イ
j = 10
1回目
a: j ← 10 mod 2 = 0
b: NISHIN(1) ← 0 div 2 = 0
2回目
a: j ← 0 mod 2 = 0
b: NISHIN(2) ← 0 div 2 = 0
この時点で誤り。
ウ
j = 10
1回目
a: NISHIN(1) ← 10 div 2 = 5
2進数にも関わらず、最下位桁が5となるため誤り。
エ 正しい。
j = 10
1回目
a: NISHIN(1) ← 10 mod 2 = 0
b: j ← 10 div 2 = 5
2回目
a: NISHIN(2) ← 5 mod 2 = 1
b: j ← 5 div 2 = 2
3回目
a: NISHIN(3) ← 2 mod 2 = 0
b: j ← 2 div 2 = 1
4回目
a: NISHIN(4) ← 1 mod 2 = 1
b: j ← 1 div 2 = 0
5回目
a: NISHIN(5) ← 0 mod 2 = 0
b: j ← 0 div 2 = 0
6回目
a: NISHIN(6) ← 0 mod 2 = 0
b: j ← 0 div 2 = 0
7回目
a: NISHIN(7) ← 0 mod 2 = 0
b: j ← 0 div 2 = 0
8回目
a: NISHIN(8) ← 0 mod 2 = 0
b: j ← 0 div 2 = 0
| 目次 | 問2 |