平成29年度 春期 高度情報技術者試験問題と解説
問3
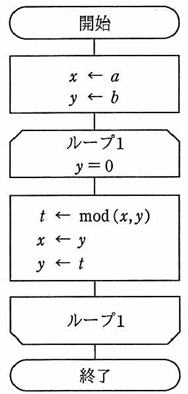
次の流れ図の処理で、終了時の x に格納されているものはどれか。ここで、与えられたa、b は正の整数であり、mod(x,y)は x を y で割った余りを返す。
ア a と b の最小公倍数
イ a と b の最大公約数
ウ a と b の小さい方に最も近い素数
エ a と b で割った商
正解
イ
解説
答えが仮に、最大公倍数になっても、計算が面倒にならないように
a = 8, b = 6 として流れ処理に当てはめてみる。
x = 8, y = 6
--- ループ1回目 ---
t = mod(8,6) = 2
x = 6
y = 2
--- ループ2回目 ---
t = mod(6,2) = 0
x = 2
y = 0
終了
x に格納された数字は2であり、8と6の最大公約数であることが分る。
従って、a と b の最大公約数であることが分る。
なお、問題のアルゴリズムは、ユークリッドの互助法と呼ばれる。
| 問2 | 目次 | 問4 |