技術士試験(情報工学部門)・情報技術者試験。ファーストマクロ。

問１

nビットの値 L₁、L₂がある。次の操作によって得られる値L₃は、L₁とL₂に対するどの論理演算の結果と同じか。

〔操作〕
(1) L₁とL₂のビットごとの論理和をとって、変数Xに記憶する。
(2) L₁とL₂のビットごとの論理積をとって更に否定をとり、変数Yに記憶する。
(3) XとYのビットごとの論理積をとって、結果をL₃とする。

---

正解

ア

---

解説

(1) より X ＝ L₁ ∪ L₂
(2) より Y ＝ NOT(L₁ ∩ L₂)
(3) より L₃ ＝ X ∩ Y

L₃ ＝ X ∩Y
＝ (L₁ ∪ L₂) ∩ NOT(L₁ ∩ L₂)
＝ (L₁ ∪ L₂) ∩ (NOT(L₁) ∪ NOT(L₂))
＝ ((L₁ ∪ L₂) ∩ NOT(L₁)) ∪ ((L₁ ∪ L₂) ∩ NOT(L₂))
＝ ((L₁ ∩ NOT(L₁)) ∪ (L₂ ∩ NOT(L₁)))
　　　　　　　∪ ((L₁ ∩ NOT(L₂)) ∪ (L₂ ∩ NOT(L₂)))
＝ (φ ∪ (L₂ ∩ NOT(L₁))) ∪ ((L₁ ∩ NOT(L₂)) ∪ φ)
＝ (L₂ ∩ NOT(L₁)) ∪ (L₁ ∩ NOT(L₂))　

従って、排他的論理和となり、アが正解である。

【別解】
下図で、
(1) は Y1、Y2、Xの部分
(2) は Y1、Y2、Y3の部分
(3) は (1) と (2) の共通部分だから Y1とY2の部分で、これは排他的論理和である。

　

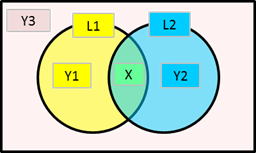
イの排他的論理和の否定は、X、Y3の部分。
ウの論理積の否定は、Y1、Y2、Y3の部分。
エの論理和の否定は、Y3の部分。

目次

問２

---