平成27年度 秋期 応用情報技術者試験問題と解説
問6
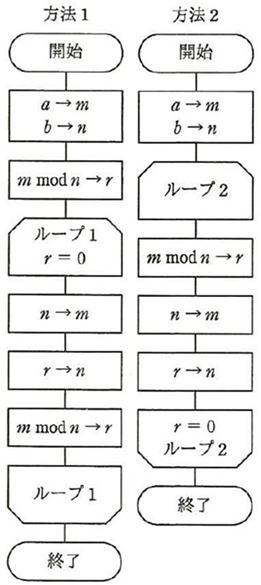
次に示すユークリッド互助法 (方法1、方法2) で、正の整数a 、b の最大公約数は、それぞれ m と n のどちらの変数に求まるか。 ここで、m
mod n は m を n で割った余りを表す。
┌───┬───┐
│方法1│方法2│
┌─┼───┼───┤
│ア│ m │ m │
├─┼───┼───┤
│イ│ m │ n │
├─┼───┼───┤
│ウ│ n │ m │
├─┼───┼───┤
│エ│ n │ n │
└─┴───┴───┘
正解
ウ
解説
a = 8, b = 6 として流れ処理に当てはめてみる。
【方法1】
8 → m, 6 → n
8 mod6 = 2 → r
--- ループ1回目 ---
6 → m
2 → n
6 mod 2 = 0 → r
終了
m = 6, n = 2 であり、
最大公約数は n に求まる。
【方法2】
8 → m, 6 → n
--- ループ1回目 ---
8 mod 6 = 2 → r
6 → m
2 → n
--- ループ2回目 ---
6 mod 2 = 0 → r
2 → m
0 → n
終了
m = 2, n = 0 であり、最大公約数は m に求まる。
したがって正解は、ウである。
| 問5 | 目次 | 問7 |