平成27年度 秋期 応用情報技術者試験問題と解説
問2
集合A、B、Cに対して A∪B∪C が空集合であるとき、包含関係として適切なものはどれか。ここで、∪は和集合を、∩は積集合を、XはXの補集合を、また、X⊆Y はXがYの部分集合であることを表す。
ア (A∩B) ⊆ C
イ (A∩B) ⊆ C
ウ (A∩B) ⊆ C
エ (A∩B) ⊆ C
正解
エ
解説
A∪B∪C = A∩B∩Cであり、下図の⑧の部分である。
これが空集合である。
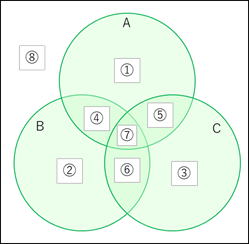
ア A∩B は④⑦の部分であり、④の部分がCの部分集合になっていない。
イ A∩B は①⑤の部分であり、①の部分がCの部分集合になっていない。
ウ A∩B は②⑥の部分であり、②の部分がCの部分集合になっていない。
エ 正しい。A∩B は、③の部分であり、Cの部分集合である。
| 問1 | 目次 | 問3 |