平成22年度 春期 応用情報技術者試験問題と解説
問6
指定された点が指定された多角形の内部にあるか外部にあるかを判定したい。多角形のすべての辺について、点から水平に延ばした半直線との交差回数を調べる。点Aのように交差回数が奇数回ならば内部、点Bのように交差回数が偶数回又は0ならば外部とする。点Cのように半直線が多角形の頂点上を通過する場合、二つの辺の端点 (上端又は下端) と交差することになるが、このときの交差回数の数え方として、適当なものはどれか。ここで、多角形には水平な辺はないものとし、辺の上の点は考えない。
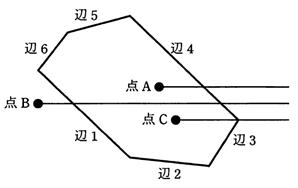
ア それぞれの辺について、下端での交差は0回、上端での交差は1回とし、合計したものを交差回数とする。
イ 二つの辺それぞれを0回とし、交差回数には加えない。
ウ 二つの辺それぞれを0.5回、つまり合計で1回の交差回数とする。
エ 二つの辺それぞれを1回、つまり合計で2回の交差回数とする。
正解
ア
解説
ア 正しい。辺2と辺3が交差する点の左側に、交差する点と水平な点、点Dがあるとすると、点Dについては、交差回数は0回となり、外部と判定される。
同様に、辺4と辺5が交差する点の左側に、交差する点と水平な点、点Eがあるとすると、点Eについては、交差回数は2回となり、外部と判定される。
イ 点Cについては交差回数が0回となり、外部と判定される。
ウ 辺2と辺3が交差する点の左側に、交差する点と水平な点、点Dがあるとすると、点Dについては、交差回数は1回となり、内部と判定される。
同様に辺4と辺5が交差する点の左側に、交差する点と水平な点、点Eがあるとすると、点Eについては、交差回数は1回となり、内部と判定される。
エ 点Cについては交差回数が2回となり、外部と判定される。
| 問5 | 目次 | 問7 |