平成22年度 春期 高度情報技術者試験問題と解説
問2
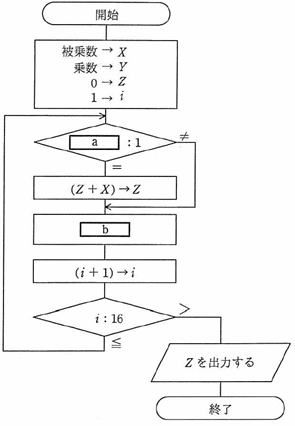
流れ図は、シフト演算と加算の繰返しによって、2進整数の乗算を行う手順を表したものである。この流れ図中のa、bの組合せとして、適切なものはどれか。ここで、乗数と被乗数は符号なしの16ビットで表される。X、Y、Z
は32ビットのレジスタであり、けた送りには論理シフトを用いる。 最下位ビットを第0ビットと記す。
┌───────┬────────────────────┐
│ a │ b │
┌─┼───────┼────────────────────┤
│ア│Yの第 0ビット│Xを1ビット左シフト、Yを1ビット右シフト│
├─┼───────┼────────────────────┤
│イ│Yの第 0ビット│Xを1ビット右シフト、Yを1ビット左シフト│
├─┼───────┼────────────────────┤
│ウ│Yの第15ビット│Xを1ビット左シフト、Yを1ビット右シフト│
├─┼───────┼────────────────────┤
│エ│Yの第15ビット│Xを1ビット右シフト、Yを1ビット左シフト│
└─┴───────┴────────────────────┘
正解
ア
解説
XとYに適当な数値を当てはめて、実際にトレースしてみる。
X=5、Y=3として、5×3で答えが15になるかどうかを考える。
X = 5 = (101)2
Y = 3 = (11)2
である。
また左シフトすると数値は2倍になり、右シフトすると2分の1 (端数は切り捨て) となることを踏まえる。
ア 正しい。
【1回目のループ】
Y=3の第0ビットが1だから Z+X = 0+5 = 5 → Z
X=5を1ビット左シフトして 10 → X
Y=3を1ビット右シフトして 1 → Y
i に1を加えて 2 →i
【2回目のループ】
Y=1の第0ビットが1だから Z+X=5+10=15 → Z
X=10を1ビット左シフトして 20 → X
Y=1を1ビット右シフトして 0 → Y
i に1を加えて 3 →i
【3回目のループ】
Y=0の第0ビットが0だから Zは15のまま。
X=20を1ビット左シフトして 40 → X
Y=0を1ビット右シフトして 0 → Y
i に1を加えて 4 →i
以降、Yの第0ビットは1になることはなく、Zは15のままループ終了。
正しい結果が得られる。
イ
【1回目のループ】
Y=3の第0ビットが1だから Z+X=0+5=5 → Z
X=5を1ビット右シフトして 2 → X
Y=3を1ビット左シフトして 6 → Y
i に1を加えて 2→i
【2回目のループ】
Y=6の第0ビットが0だから Zは5のまま。
X=2を1ビット右シフトして 1 → X
Y=6を1ビット左シフトして 12 → Y
i に1を加えて 3→i
【3回目のループ】
Y=12の第0ビットが0だから Zは5のまま。
X=1を1ビット左シフトして 0 → X
Y=12を1ビット右シフトして 24 → Y
i に1を加えて 4→i
以降、Yの第0ビットは1になることはなく、Zは5のままループ終了。
ウ
【1回目のループ】
Y=3の第15ビットが0だから Zは0のまま。
X=5を1ビット左シフトして 10 → X
Y=3を1ビット右シフトして 1 → Y
i に1を加えて 2 →i
【2回目のループ】
Y=1の第15ビットが0だから Zは0のまま。
X=10を1ビット左シフトして 20 → X
Y=1を1ビット右シフトして 0 → Y
i に1を加えて 3 →i
【3回目のループ】
Y=0の第15ビットが0だから Zは0のまま。
X=20を1ビット左シフトして 40 → X
Y=0を1ビット右シフトして 0 → Y
i に1を加えて 4 → i
以降、Yの第0ビットは1になることはなく、Zは0のままループ終了。
エ
【1回目のループ】
Y=3の第15ビットが0だから Zは0のまま。
X=5を1ビット右シフトして 2 → X
Y=3を1ビット左シフトして 6 → Y
i に1を加えて 2 →i
【2回目のループ】
Y=6の第15ビットが0だから Zは0のまま。
X=2を1ビット右シフトして 1 → X
Y=6を1ビット左シフトして 12 → Y
i に1を加えて 3 →i
【3回目のループ】
Y=12の第15ビットが0だから Zは0のまま。
X=1を1ビット左シフトして 0 → X
Y=12を1ビット右シフトして 24 → Y
i に1を加えて 4 →i
以降、Xが0になったので、Zに加算されることはなく、Zは0のままループ終了。
| 問1 | 目次 | 問3 |