平成22年度 秋期 応用情報技術者試験問題と解説
問7
正の整数Mに対して、次の二つの流れ図に示すアルゴリズムを実行したとき、結果x の値が等しくなるようにしたい。aに入れる条件として、適切なものはどれか。
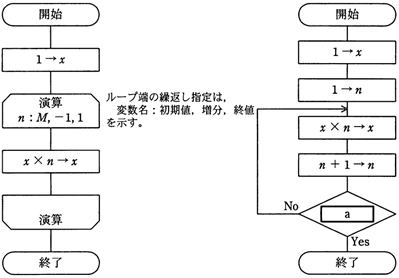
ア n < M
イ n > M−1
ウ n > M
エ n > M+1
正解
ウ
解説
問題の左の流れ図のループの部分は、「nの値をMから初めて一つずつ減らし、1になるまで繰り返す」という意味である。
変数x は1で初期化されているため、ループ内でx の値は、以下のように変わっていく。
1回目 1×M = M
2回目 M×(M−1)
3回目 M×(M−1)×(M−2)
・・・
M回目 M×(M−1)×(M−2)×・・・×1 = M!
問題の右の流れ図のループの部分はループ内で x の値は、以下のように変わっていく。
1回目 1×1=1 (n=2)
2回目 1×(1+1) (n=3)
3回目 1×(1+1)×(1+2) (n=4)
・・・
M−1回目 1×(1+1)×(1+2)×・・・×(M−1) = (M−1)! (n=M)
M回目 1×(1+1)×(1+2)×・・・× M = M! (n=M+1)
従って、M回ループするように a で制御するため n > M が条件となる。
| 問6 | 目次 | 問8 |