平成21年度 秋期 高度情報技術者試験問題と解説
問3
n個の要素x1, x2, …, xnから成る連結リストに対して、新たな要素xn+1の末尾への追加に要する時間をf(n)とし、末尾の要素xnの削除に要する時間をg(n)とする。nが非常に大きいとき、実装方法1と実装方法2におけるg(n)/f(n)の挙動として、適切なものはどれか。
〔実装方法1〕
先頭のセルを指すポインタ型の変数frontだけをもつ。
![]()
〔実装方法2〕
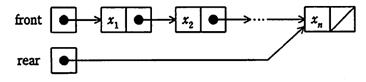
先頭のセルを指すポインタ型の変数frontと、末尾のセルを指すポイント型の変数rearを併せもつ。
┌─────────┬─────────┐
│ 実装方法1 │ 実装方法1 │
┌─┼─────────┼─────────┤
│ア│ほぼ1になる。 │ほぼ1になる。 │
├─┼─────────┼─────────┤
│イ│ほぼ1になる。 │ほぼnに比例する。│
├─┼─────────┼─────────┤
│ウ│ほぼnに比例する。│ほぼ1になる。 │
├─┼─────────┼─────────┤
│エ│ほぼnに比例する。│ほぼnに比例する。│
└─┴─────────┴─────────┘
正解
イ
解説
連結リストをたどって、対象となるセルにたどりつくまでの時間を等考える問題である。
〔実装方法1〕
nが非常に大きいため、
x1から順に連結リストをたどって、xnにたどりつく時間も、xn+1にたどりつく時間もほとんど変わらない。
したがって、g(n)/f(n) ≒ 1である。
〔実装方法2〕
x1から順に連結リストをたどって、xnにたどりつき、末尾の要素xnの削除に要する時間はnに比例する。
しかし、末尾のxn+1にたどりつくには、変数rearによって1回で済む。
したがって、g(n)/f(n) はnに比例する。
| 問2 | 目次 | 問4 |