令和3年度 技術士第一次試験問題【専門科目】
Ⅲ-4
各ノード間の移動コストが非負である場合の最短経路探索を行う際、Dijkstra のアルゴリズムがよく用いられる。Dijkstra のアルゴリズムを用いて下図の始点ノードSから他のノードへの最短経路・コストを求める際に、Sからの最短経路が決定していくノードの順序として、最も適切なものはどれか。
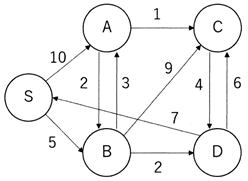
① S A B C D
② S A C B D
③ S B A D C
④ S B D A C
⑤ S B C A D
正解
④
解説
Dijkstra (ダイクストラ) のアルゴリズムは、各点までの距離を順番に確定していくアルゴリズムのことである。
手順は以下のとおりである。
(1) 始点を決め、始点のコストを0、始点以外の全てのノードまでのコストを最大値で初期化する。
(2) 始点を確定済みとし、始点に移動する。
(3) 移動したノードと隣接している未確定のノードまでの、始点からのコストをそれぞれ求め、それぞれを最小値で更新する。
(4) 未確定ノードの中から最小のコストのノードを確定済みとし、そのノードに移動する。
(5) (3),(4)を未確定ノードがなくなるまで繰り返す。
Sからの最短経路が決定していくノードの順序は以下のとおりである。
1) S:0、A:∞、B:∞、C:∞、D:∞ で初期化する。
2) Sを確定済みとし、Sに移動する。
3) Sと隣接しているA、Bまでの、始点からのコストを求め、A:10、B:5 として更新する。
4) 未確定ノードの中から最小のノードであるBを確定済みとし、Bに移動する。
5) Bと隣接しているA、C、Dまでの、始点からのコストをそれぞれ求め、A:8、C:14、D:7として更新する。
6) 未確定ノードの中から最小のノードであるDを確定済みとし、Dに移動する。
7) Dと隣接しているCまでの、始点からのコストをそれぞれ求め、C:13として更新する。
8) 未確定ノードの中から、最小のコストであるAを確定済みとし、Aに移動する。
9) Aと隣接している未確定ノードはない。
10) 唯一残った未確定ノードCを確定済みとする。
したがって、S ⇒ B ⇒ D ⇒ A ⇒ Cの順に最短経路が決定していく。
| Ⅲ-3 | 目次 | Ⅲ-5 |