平成30年度 技術士第一次試験問題【専門科目】
Ⅲ-12
同次座標を使った画像のアフィン変換に関して、位置 (x、y) を反時計回りに90度回転させた後、x軸正方向に+30ピクセル平行移動する変換行列として、最も適切なものはどれか。
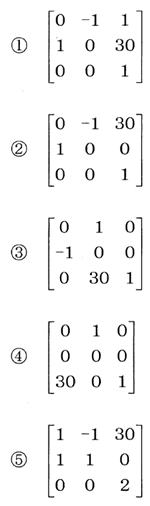
正解
②
解説
アフィン変換は、図形を回転させたり、平行移動したり、拡大縮小したりする変換のことである。
点 (x, y) を原点の周りに角θだけ回転し、点 (x', y') に移動すると
x' = x・cosθ - y・sinθ
y' = x・sinθ + y・cosθ
となる。
さらに、x軸方向に+30ピクセル平行移動し、点 (x'', y'') に移動すると
x'' = x・cosθ- y・sinθ+30
y'' = x・sinθ + y・cosθ
となる。
題意より、θ = 90°であるから、sinθ = 1、cosθ = 0である。
従って、
x'' = x・0 - y・1 + 30 = x・0 + y・(-1) + 30
y'' = x・1 + y・0 + 0
| Ⅲ-11 | 目次 | Ⅲ-13 |