技術士試験(情報工学部門)・情報技術者試験。ファーストマクロ。

問２３

1桁の2進数A、Bを加算し、Xに桁上がり、Yに桁上がりなしの和 (和の1桁目) が得られる論理回路はどれか。

---

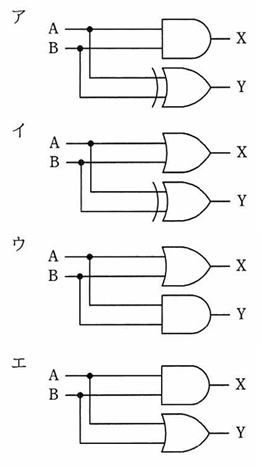
正解

ア

---

解説

題意より、以下のとおり出力される論理回路となる。
(A, B) = (0, 0) の時、0＋0 = 0 より (X, Y) = (0, 0)
(A, B) = (0, 1) の時、0＋1 = 1 より (X, Y) = (0, 1)
(A, B) = (1, 0) の時、1＋0 = 1 より (X, Y) = (0, 1)
(A, B) = (1, 1) の時、1＋1 = 10₍₂₎ より (X, Y) = (1, 0)

Xに注目すると
(A, B) = (0, 0) の時、0
(A, B) = (0, 1) の時、0
(A, B) = (1, 0) の時、0
(A, B) = (1, 1) の時、1
つまり　論理積素子 (AND) 回路である。

Yに注目すると
(A, B) = (0, 0) の時、0
(A, B) = (0, 1) の時、1
(A, B) = (1, 0) の時、1
(A, B) = (1, 1) の時、0
つまり　排他的論理和素子 (XOR) 回路である。

問２２

目次

問２４

---